个不同的事物有
种不同的排列方法。

本文介绍的对称群(Symmetric Groups),可从排列中很自然的产生。凯莱定理(Cayley's theorem)说:排列——这种工具足够强大,可用来建立任意群。

Arthur Cayley (1821-1895)假设有5个对象,可用以下形式来表示排列第
和第
个元素对换:
,第1行是从1到5的序号,第2行是重新排列后的顺序。如果视排列为函数
,第一行为输入,第二行为输出。那么排列
与排列
的续贯操作,就如同函数组合(function composition)
。比如:排列
与
续贯操作等于
。注意函数组合是从右向左的,以1为例:
;以2为例:
.
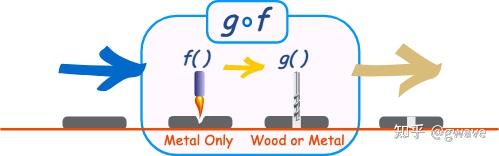
来源:https://www.mathsisfun.com/sets/functions-composition.html这种表示方法不够高效,下面将介绍更简洁的循环表示法,以
为例,
,表示为
;
,表示为
,整体表示为
,称为循环分解(cycle decomposition)。
由3个元素组成,称为“3-cycle”,
由两个元素组成,称为“2-cycle”,“2-cycle”也称换位(Transposition)。
若两个cycle没有重复的元素,则它们的顺序可互换,如:
。
若两个cycle存在重复元素,则不能互换顺序,如
,LHS:
; RHS:
.
对上例略作变化:
可以表示为:
,注意到其中包含了2个1-cycle:
,由于1-cycle没进行任何改变,故可略去不写,故最终结果可表示为
。其实,未必要从
开始,也可从
开始,于是:结果表达为
;同样的,如果从
开始,结果表示为
,上面3个cycle是等价的。习惯上,选择最小的数作为开始,本例为
。
排列与群的概念很吻合,在“群的定义”一文中,我们定义了群的概念如下,逐条对下,排列都满足:
群G(Group)的元素属于一个集合
如果对一个特定collection中的元素进行排列,比如数字1,2,3,得到了一个包含
个元素的集合,下面几点可以自行考虑下;G对应的二元操作(Binary Operation)以
表示;封闭性(Closed under operation): 对G的两个元素进行任何操作,结果仍在集合内,即:
for all
;恒等元(Identity): 存在一个元素
,
; 逆(Inverse): 对每一个
的元素
,都存在一个元素
,使得
;
每种排列都可逆;结合律(Associativity):
.
个对象所有的重新排列组成对称群
,
表示对称 Symmetric.
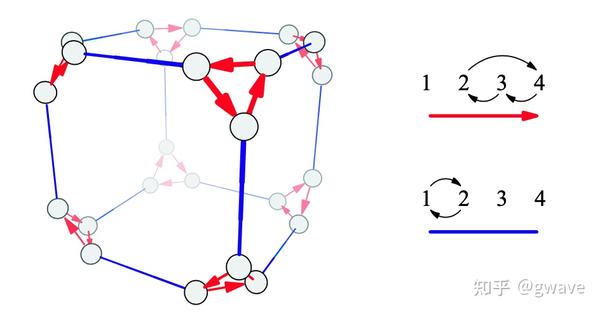
S4的凯莱图 来源:Visual Group Theory上图是
的凯莱图,为了不太拥挤,具体数字没有标。
共
个对象,其凯莱图是被“砍掉”8个角的立方体,被称为“Truncated Cube”。
虽然对
个对象进行排列构成一个群,但是建立一个排列群并非一定需要所有的排列,通常
的子集就可以构成群,一种著名的方法就是取一半
的元素,构成交错群
,但是并非随意选一半都能构成群,但如果选取
中每个元素并对其进行平方,平方后得到的元素整好是
的一半,称为交错群(Alternating Group)
。
下图说明了
的形成过程,左边是
,右边是平方后的元素,6个元素中的4个相同,都是恒等元素,什么变化都不做(2个元素交换两次,打回原形),故右侧实际包含3个不变的元素,是左边的一半,这三个元素就是
。
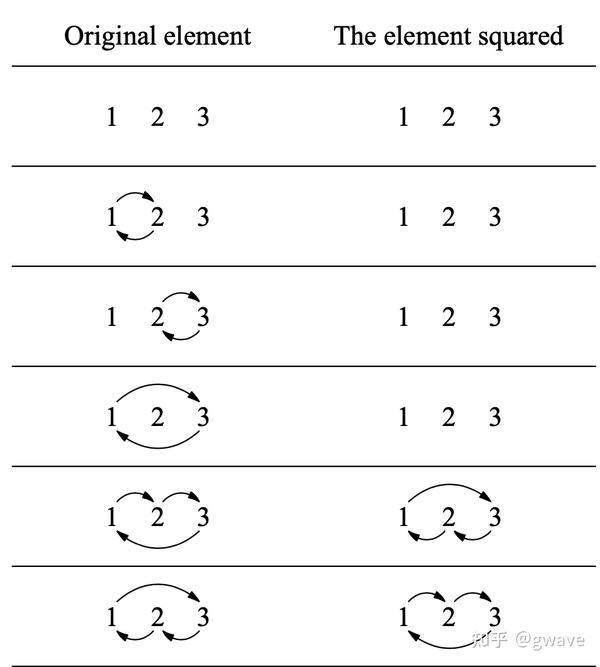
A3 来源:Visual Group Theory题图是柏拉图固体(Platonic solids),柏拉图固体是种三维的多面体,其中每个面都是(每个角相等,每条边相等)正多边形。柏拉图固体只有图中的5种(可证明)。
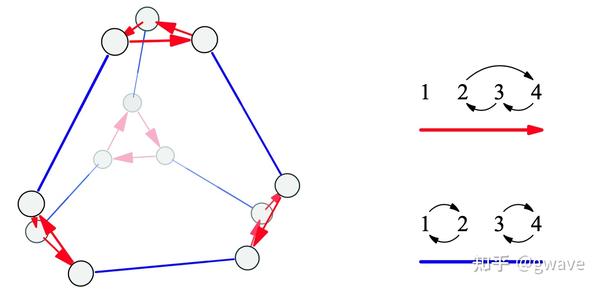
A4的凯莱图 来源:Visual Group Theory四面体的对称群是
,包含了4个对象所有排列的一半。
立方体和八面体都对应同一个对称群
,这也是为什么
的凯莱图类似立方体的原因。
十二面体和二十面体都对应同一个对称群
,其大小为
,可分别以“砍角的”十二面体和二十面体来显示。
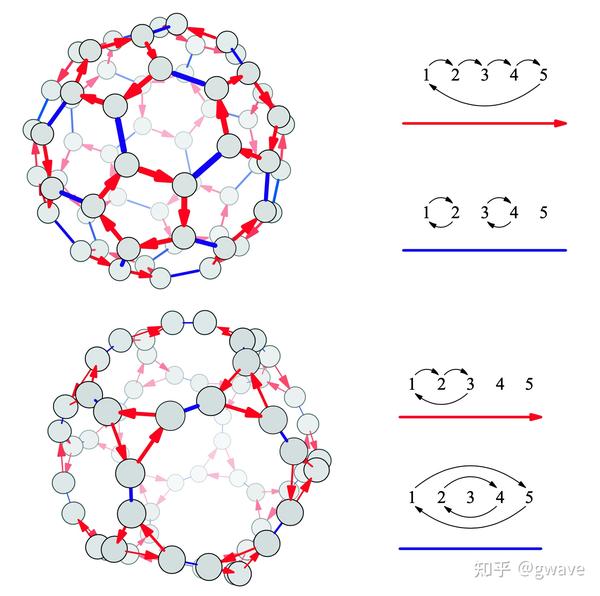
A5的凯莱图 来源:Visual Group Theory
第四次庄家抓牌的第一和第三幢的上面一张,第二家拿第一幢的下面一张,第三家拿第二幢的上面一张,第四家拿第二幢的下面一张。
三摊:如果一家吃碰杠在牌面上有三次博彩问答,并且三次都是同一色或者两字碰加任何一色或一字碰加同一色的